
1. 그래프
그래프(Graph)는 정점(Vertex)과 간선(Edge)로 구성된 구조입니다.
예를 들어 전철 노선도는 각 지점을 선으로 연결한 그래프라고 볼 수 있습니다.
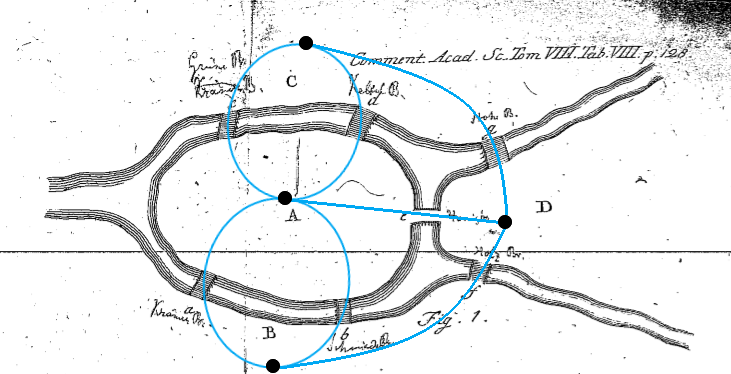
그래프 이론은 1736년 오일러(Euler)가 쾨니히스베르크(Koenigsberg)의 다리 문제를 풀기 위해 적용하면서 정립되었습니다.
현재는 전기 회로의 분석, 최단거리 검색, 컴퓨터 네트워크, 인공지능 등에 광범위하게 이용되고 있습니다.
그래프(G)는 순서쌍 G=(V, E)로 나타내며, V는 정점, E는 간선을 의미합니다.
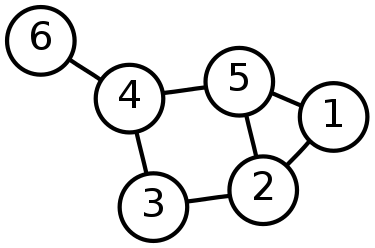
위 그래프는 6개의 정점과 7개의 간선으로 이루어진 그래프이며 다음과 같이 나타낼 수 있습니다.
V(G) = {1, 2, 3, 4, 5, 6} E(G) = {(1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (4, 5), (4, 6)}
두 정점의 쌍에 순서가 없으면 무방향 그래프(Undirected Graph), 순서가 있으면 방향 그래프(Directed Graph)라고 합니다.
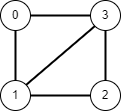
위 그래프는 무방향 그래프이며, (V0, V1) = (V1, V0) 입니다.
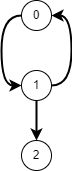
위 그래프는 방향 그래프이며, V0 -> V1는 <V0, V1> 로 나타내고 <V0, V1> ≠ <V1, V0> 입니다.
최대 수의 간선을 가진 그래프는 완전 그래프(Complete Graph)라또는 연결라고 합니다.
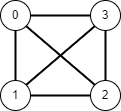
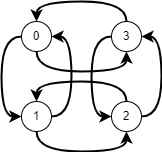
완전 그래프는 정점이 n개 일때 무방향 그래프는 n(n-1)/2 개, 방향 그래프는 n(n-1) 개의 간선을 가집니다. 예를 들어 정점이 4개라면 무방향 그래프에서는 4*3 / 2 = 6개, 방향 그래프에서는 4*3 = 12개의 간선을 가집니다.
2. 그래프의 표현
그래프는 인접 행렬(Adjacency Matrix) 또는 인접 리스트(Adjacency List)로 표현할 수 있습니다.

위의 무방향 그래프를 인접 행렬로 나타내면 다음과 같습니다. 
G = [[0, 1, 0, 1], [1, 0, 1, 1], [0, 1, 0, 1], [1, 1, 1, 1]]
인접 리스트의 경우 다음과 같습니다.
G = [[1, 3], [0, 2, 3], [1, 3], [0, 1, 2]]
방향 그래프도 동일하게 나타냅니다.

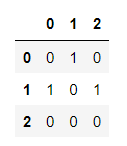
G = [[0. 1. 0], [1, 0, 1], [0, 0, 0]]
G = [[1], [0, 2]]
3. 그래프 탐색
입력받은 그래프를 컴퓨터가 알기 위해서는 그래프 탐색이 필요합니다. 그래프를 탐색하는 방법에는 깊이 우선 탐색(Depth-First Search, DFS)과 넓이 우선 탐색(Breadth-First Search, BFS)이 있습니다.
DFS는 하나의 정점으로부터 최대한 깊이 탐색 후 다시 돌아가서 다른 경로를 탐색하는 방법입니다.
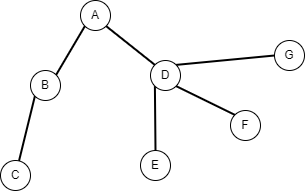
출발점이 A라고 한다면 A -> B -> C -> D -> E -> F -> G 순서로 탐색을 합니다.
BFS는 하나의 정점으로부터 가까운 정점을 우선 탐색하는 방법입니다. 출발점이 A라고 한다면 A -> B -> D -> C -> E -> F -> G 순서로 탐색을 합니다.
모든 경로를 탐색할 필요가 있다면 DFS를, 최단경로를 찾는다면 BFS를 사용하면 됩니다.
4. 파이썬 연습
파이썬을 통해 DFS와 BFS를 구현해보겠습니다.

DFS는 스택이나 재귀함수를 통해 구현가능합니다.
우선 A를 스택에 넣습니다. search = [] stack = ["A"]
스택에서 A를 꺼내서 탐색을 합니다. A와 연결된 B와 D를 스택에 넣습니다. B부터 탐색하기위해 D, B 순서로 넣습니다. (B, D 순서로 넣어도 됩니다.) search = ["A"] stack = ["D", "B"]
스택에서 B를 꺼내어 탐색합니다. B와 연결된 C를 스택에 넣습니다. search = ["A", "B"]
stack = ["D", "C"]
스택에서 C를 꺼내어 탐색합니다. search = ["A", "B", "C"]
stack = ["D"]
스택에서 D를 꺼내어 탐색합니다. D와 연결된 E, F, G를 스택에 넣습니다. search = ["A", "B", "C", "D"]
stack = ["G", "F", "E"]
스택이 빌때까지 차례대로 꺼내어 탐색을 합니다. search = ["A", "B", "C", "D", "E", "F", "G"]
stack = []

재귀함수를 통해 DFS를 구현할 수도 있습니다.

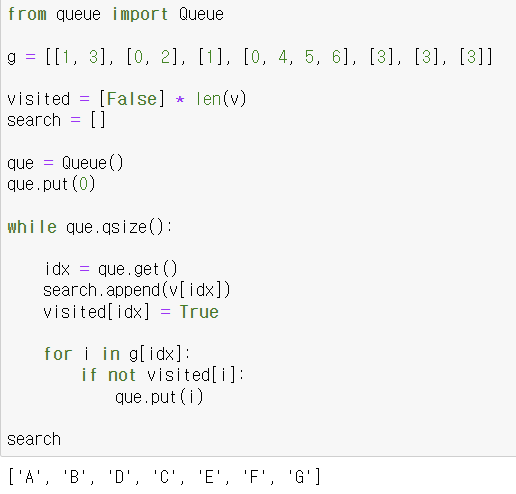
다음으로 BFS를 구현하겠습니다. BFS는 큐를 통해 구현가능합니다.
우선 A를 큐에 넣습니다. search = [] que = ["A"]
큐에서 A를 꺼내서 탐색을 합니다. A와 연결된 B와 D를 큐에 넣습니다. B부터 탐색하기위해 B, D 순서로 넣습니다. (D, B 순서로 넣어도 됩니다.) search = ["A"] que = ["B", "D"]
큐에서 B를 꺼내어 탐색합니다. B와 연결된 C를 큐에 넣습니다. search = ["A", "B"]
que = ["D", "C"]
큐에서 D를 꺼내어 탐색합니다. D와 연결된 E, F, G를 큐에 넣습니다. search = ["A", "B", "D"] que = ["C", "E", "F", "G"]
큐가 빌때까지 차례대로 꺼내어 탐색을 합니다. search = ["A", "B", "D", "C", "E", "F", "G"] que = []
|
 스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟