라즈베리파이반

역전파 알고리즘은 input과 output을 알고 있는 상태에서 신경망을 학습시키는 알고리즘입니다.

단일 뉴런에서는 다음과 같이 순방향(Forwardpass)으로 계산이 됩니다.

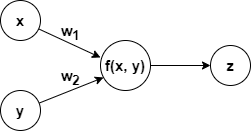
순방향 계산으로부터 우리는 f(x, y)에 대한 x의 편미분값과 y의 편미분값을 구할 수 있습니다.

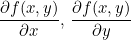
이 값을 Local Gradient라고 합니다.

순방향을 통해 ouput을 구했다면 오차 L을 구할 수 있습니다. 오차 L로부터 역방향(Backwardpass)으로 편미분값을 구할 수 있습니다. 

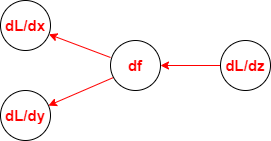
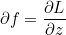
이 값을 Global Gradient라고 합니다. 

우리는 역방향으로 오차에 대한 x와 y의 편미분값을 구해야 합니다. 이는 Chain Rule을 통해 다음과 같이 계산될 수 있습니다.

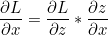
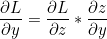
z = f(x, y) 이므로 각각의 편미분값은 Local Gradient * Global Gradient 와 같다는 것을 알 수 있습니다.

이제 은닉층을 포함한 심층 신경망을 통해 계산을 해보겠습니다.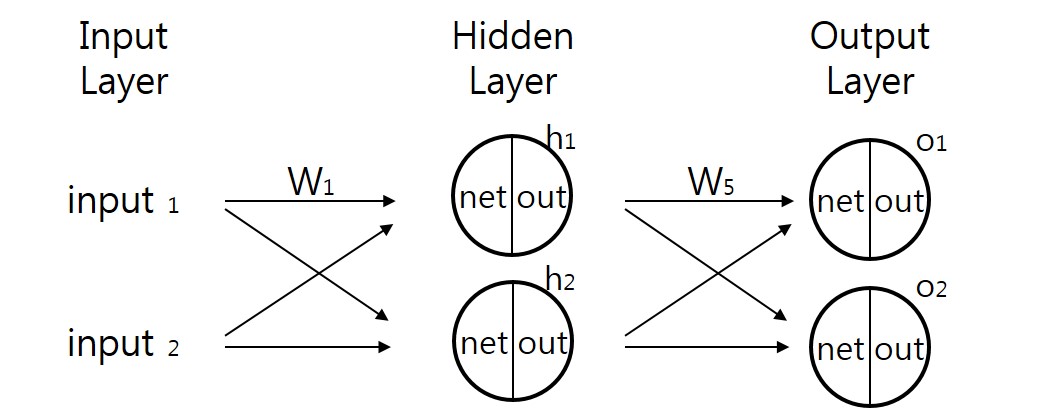

미분을 해야하므로 미분이 불가능한 계단함수 대신 활성함수로 로지스틱 함수를 사용하겠습니다.

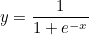
전송함수값은 net, 활성함수값은 out으로 표시했습니다. 우선 출력값에서 가까운 가중치 w₅ ~ w₈ 을 갱신하도록 하겠습니다. 

w₅를 기준으로 설명하겠습니다. w₅^​+​ 가 갱신값이라고 한다면 다음과 같은 식이 성립합니다.

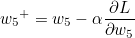
α 는 하이퍼 파라미터 학습률(Learning Rate)이며, 우리는 오차에 대한 편미분값을 구해야합니다. 위에 설명했듯이 Chain Rule 을 통해 Local Gradient 와 Global Gradient를 순차적으로 곱하면 됩니다.

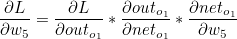
오차 L은 o₁의 오차와 o₂의 오차의 합의 평균과 같습니다.

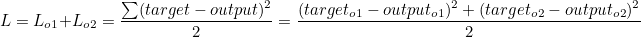
그러므로 오차에 대한 out_o1 의 편미분값은 다음과 같습니다.

out_o1 ​은 로지스틱 함수이므로 out_o1 ​에 대한 net_o1​ 의 편미분값은 로지스틱 함수를 미분한 값과 같습니다.

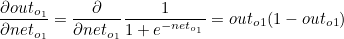
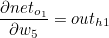
이때 첫번째 계산값과 두번째 계산값의 곱은 이후에 사용되므로 묶어서 δ_o1 이라고 한다면 다음과 같습니다.

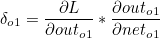
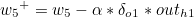
나머지도 동일하게 구할 수 있습니다.

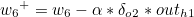
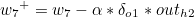
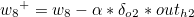
이제 가중치 w₁ ~ w₄ 을 갱신하도록 하겠습니다.
 

w₁​ 을 기준으로 설명하겠습니다.

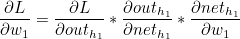
out_h1 은 o₁과 o₂ 모두에 영향을 미치므로 다음과 같이 정리할 수 있습니다.

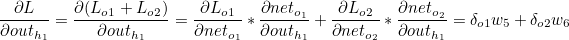
out_h1 ​은 로지스틱 함수이므로 out_h1 ​에 대한 net_h1​ 의 편미분값은 로지스틱 함수를 미분한 값과 같습니다.

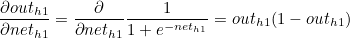
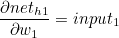
마찬가지로 첫번째 계산값과 두번째 계산값의 곱을 묶어서 δ_h1 이라고 한다면 다음과 같습니다.

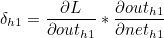
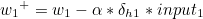
나머지도 동일하게 구할 수 있습니다.

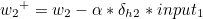
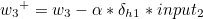
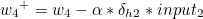
복잡해 보이지만 전체 가중치를 모두 반영하는 경사하강법의 경우 뉴런의 수가 많을수록 속도가 느려지는 반면 오차역전파 알고리즘의 경우 행렬을 통해 계산되므로 더욱 빠르게 학습을 할 수 있습니다.