
통계적 추론(statistical inference)이란 표본 통계량을 이용하여 모집단의 모수를 추론하는 과정을 말합니다. 통계적 추론은 추정(estimation)과 가설검정(testing hypothesis)으로 나눌 수 있습니다. 추정은 표본을 통해 모집단의 특성을 추측하여 신뢰구간을 형성하는 과정이고, 가설검정은 모집단의 추정값에 대한 주장에 가설을 세우고 가설을 검정하는 과정입니다.
가설검정 과정에서 사용되는 통계량을 검정 통계량이라고 합니다. 검정 통계량에는 Z-값, t-값, F-값, X2-값 등이 있습니다. 일종의 표본 통계량으로, 표본 통계량을 2차 가공한 값입니다.
통계적 가설에는 귀무가설과 대립가설이 있습니다. 귀무가설(null hypothesis)은 기존의 주장에 대한 가설이며 H0로 나타내고, 대립가설(alternative hypothesis)는 새롭게 주장하는 가설이며 H1으로 나타냅니다.
가설검정에서 귀무가설을 채택하거나 기각할때 오류(error)가 발생할 수 있는데, 여기에는 제 I종 오류(type I error)와 제 II종 오류(type II error)가 있습니다. 제 I종 오류는 귀무가설이 맞는데 틀렸다고 결론을 내리고 대립가설을 채택했을 때 발생하는 오류이고, 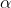 로 나타냅니다. 제 II종 오류는 틀린 귀무가설을 맞다고 결정하여 생기는 오류로서 로 나타냅니다. 제 II종 오류는 틀린 귀무가설을 맞다고 결정하여 생기는 오류로서 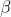 로 표시합니다. 로 표시합니다.
실제 |
귀무가설 채택 |
귀무가설 기각 |
귀무가설이 맞다 |
옳은 결정 |
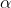 (제 I종 오류) (제 I종 오류) |
대립가설이 맞다 |
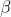 (제 II종 오류) (제 II종 오류)
|
옳은 결정 |
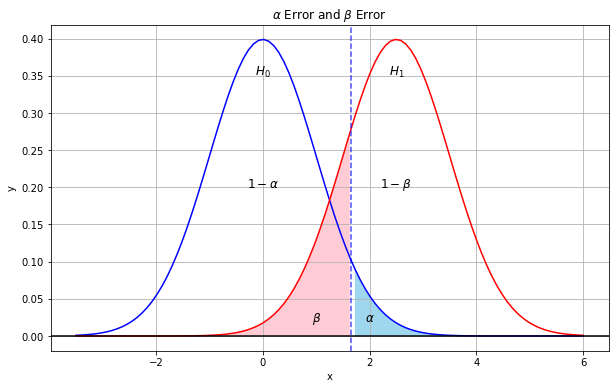
I종 오류와 II종 오류는 트레이드 오프 관계입니다. 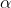 가 커지면 가 커지면 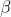 는 작아지고, 는 작아지고, 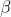 가 커지면 가 커지면 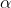 가 작아집니다. 가설검정에서 오류를 없앨 수는 없지만 표본의 크기를 늘려 표준오차를 작게 해주면 오류를 줄일 수 있습니다. 가 작아집니다. 가설검정에서 오류를 없앨 수는 없지만 표본의 크기를 늘려 표준오차를 작게 해주면 오류를 줄일 수 있습니다.
귀무가설에 대한 오류 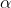 를 유의수준(significance level)이라고 합니다. 제 I종 오류가 발생할 확률의 최대치 입니다. 보통 를 유의수준(significance level)이라고 합니다. 제 I종 오류가 발생할 확률의 최대치 입니다. 보통 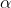 =0.05와 =0.05와 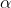 =0.01을 사용합니다. =0.01을 사용합니다.
이번 글에서는 우선 t-검정에 대해서 알아보겠습니다.
t-검정은 평균의 편차를 검정하기위해 사용하는 방법입니다. 검정에 사용하는 통계량은 t-값으로, 평균의 편차를 표준오차로 나누어 표준화한 값을 사용합니다.
t-검정은 크게 단일표본 t-검정(one sample t-test), 독립표본 t-검정(independent two sample t-test), 대응표본 t-검정(paired sample t-test) 3가지로 분류됩니다.
t-검정을 하기 위해서는 표본이 정규성(normality)을 가져야합니다. 표본의 크기가 30을 넘으면 중심극한정리에 의하여 표본의 분포가 정규분포에 가까워지므로 정규성 검정을 할 필요가 없습니다. 표본의 수가 적으면 shapiro-wilk 검정법을 통해 정규성을 가지는지 확인할 필요가 있습니다. 정규성 검정에 대해서는 따로 설명하지 않겠습니다.
1) 단일표본 t-검정(one sample t-test)
단일표본 t-검정은 단일 표본집단에서 모집단의 평균에 대한 가설을 검정하기 위해 사용합니다. 자유도는 n-1이며, t-값은 다음과 같이 계산합니다.
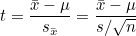
임의의 데이터 X를 만들어 단일표본 t-검정을 해보겠습니다.
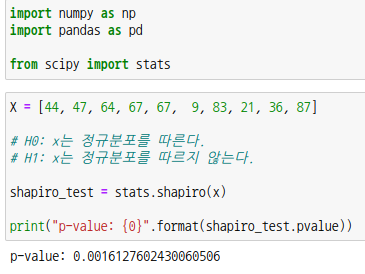
표본의 크기가 10이므로 정규성 검정을 합니다. 정규성 검정은 scipy 모듈의 shapiro 함수를 사용합니다. p-값이 유의수준 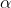 =0.05보다 크므로 귀무가설을 채택하여 x는 정규분포를 따릅니다. =0.05보다 크므로 귀무가설을 채택하여 x는 정규분포를 따릅니다.
이제 다음과 같이 가설을 세우고 t-검정을 합니다.

대립가설(H1)이 "모평균(mu)는 50이 아니다." 이므로 양측검정을 합니다.
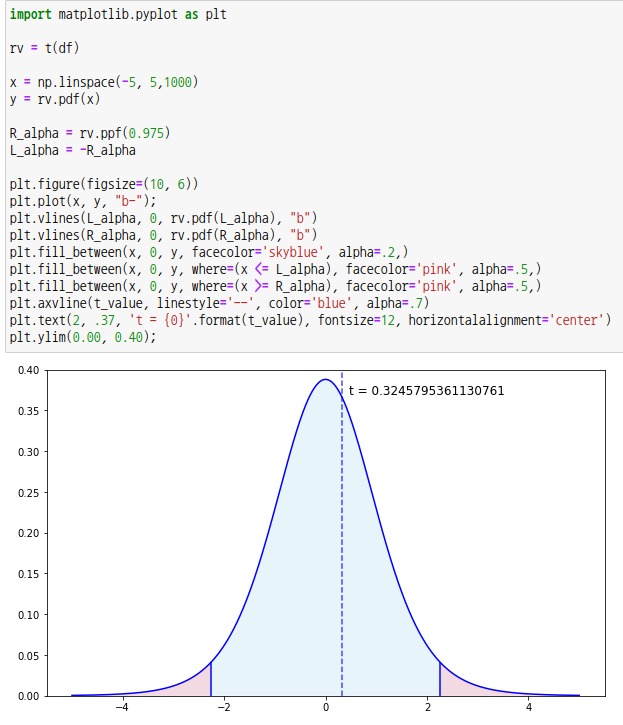
scipy 모듈의 서브패키지 t를 사용하여 t-값에 대한 p-값(확률값)을 구할 수 있습니다.
양측검정이므로 유의수준은 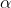 /2 를 기준으로 검정합니다. /2 를 기준으로 검정합니다. p-값이 0.025보다 크므로 귀무가설을 채택하여 모평균은 50 입니다.
scipy 모듈의 서브패키지 ttest_1samp를 이용할 수도 있습니다. 첫번째 파라미터로 표본 배열, 두번째 파라미터로 모평균(mu)을 넣어줍니다. 기본값으로 파라미터 alternative는 ‘two-sided’로 설정되어 있는데 단측검정을 하려면 'less' 또는 'greater'를 넣어주면 됩니다.
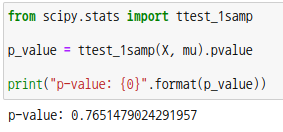
이때 p-값은 양쪽 꼬리를 더한 확률값이므로 유의수준 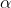 =0.05 와 비교하면 됩니다. =0.05 와 비교하면 됩니다. p-값이 0.05보다 크므로 귀무가설을 채택하여 모평균은 50 입니다.
2) 독립표본 t-검정(independent two sample t-test)
독립표본 t-검정은 서로 독립된 두 집단의 표본평균 편차를 검정합니다. t-값은 표본평균 편차를 표준오차로 나누어 표준화시킨 값입니다. 즉, t-값이 커질수록 표본평균 편차는 커집니다. 표본의 크기가 30 이상이면 t-분포는 정규분포에 가까워지므로 t-값 대신 Z-값을 사용해되 됩니다.
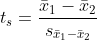
독립표본 t-검정은 두 집단에 대한 분산의 동일성 여부에 따라 스튜던트의 t-검정(Student's t-test)과 웰치의 t-검정(Welch's t-test)로 나눠집니다. 분산이 동일하다면 스튜던트의 t-검정, 분산이 다르다면 웰치의 t-검정을 사용합니다. 리베네 검정(Levene's test)을 통해 등분산성을 검정할 수 있습니다.
표본평균에 대한 분산은 다음과 같이 정의됩니다.
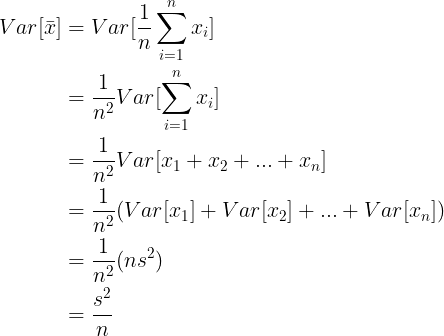
그러므로 표본평균 편차에 대한 표준오차 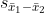 는 다음과 같습니다. 는 다음과 같습니다.
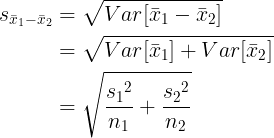
스튜던트의 t-검정에서는 두 집단의 분산이 동일합니다. 그러므로 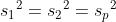 입니다. 입니다. 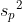 를 합동분산(pooled variance)이라고 합니다. 스튜던트의 t-검정에서 자유도는 n1 + n2 - 2 입니다. 를 합동분산(pooled variance)이라고 합니다. 스튜던트의 t-검정에서 자유도는 n1 + n2 - 2 입니다.
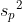 는 다음과 같습니다. 는 다음과 같습니다.
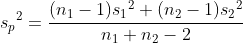
그러므로 다음과 같이 정리될 수 있습니다.
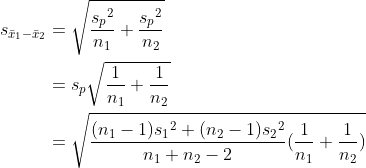
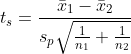
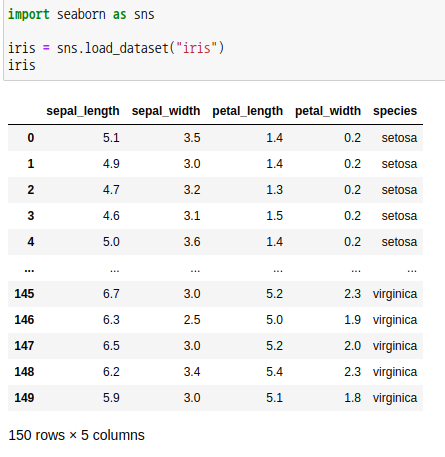
seaborn 모듈에서 iris 데이터를 불러와서 'setosa'와 'vriginica'의 각 특성을 t-검정 해보겠습니다.

분산이 같지 않으면 웰치의 t-검정을 사용합니다. t-값은 다음과 같습니다.
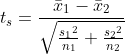
이 검정법은 자유도를 다르게 설정합니다.
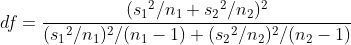
방금 전에 검정한 X1, X2를 리베네 검정을 해봅시다. scipy 모듈의 서브패키지 levene 를 통해 검정할 수 있습니다.
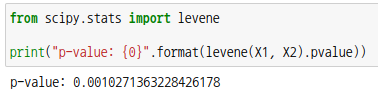
p-값이 0.05보다 작으므로 등분산이라는 귀무가설을 기각하고 등분산이 아니라는 대립가설을 채택합니다. 등분산이 아니므로 웰치의 t-검정을 하도록 하겠습니다.
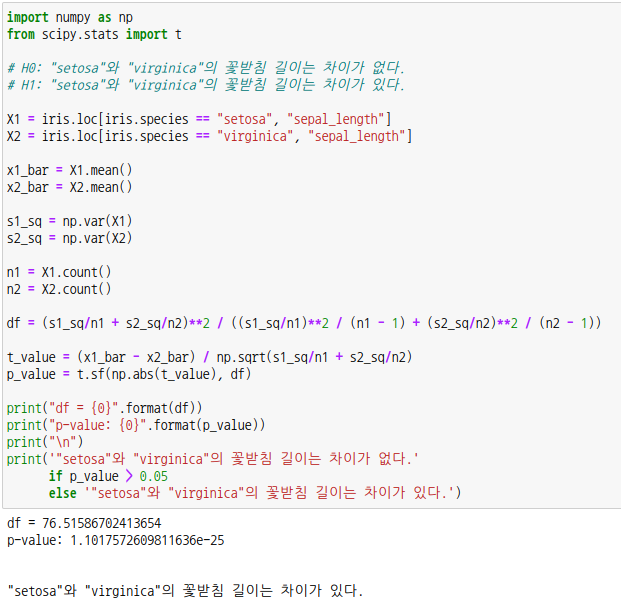
스튜던트의 t-검정으로 구한 p-값과 조금 다른 값이 나옵니다. 자유도도 정수가 아닌 실수형태로 나옵니다.
scipy 모듈에는 독립표본 t-검정을 위한 패키지도 있습니다.
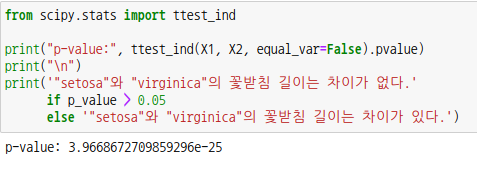
파라미터 equal_var는 기본값이 True이며, False로 설정하면 웰치의 t-검정을 사용하여 가설을 검정합니다. 직접 계산한 p-값이랑 조금 차이가 나는데 너무 작은 값이라 그런듯 합니다.
3) 대응표본 t-검정(paired sample t-test)
대응표본 t-검정은 동일한 사람이나 물건에 대한 측정값이 2개인 경우에 사용합니다. 시간상 전후의 개념이기때문에 독립된 두 집단일 필요가 업습니다. 예를 들어 다이어트 약물의 사용 전후 몸무게가 차이나는지를 검정할 수 있습니다.
두 대응집단의 편차에 대한 평균과 분산은 다음과 같습니다.
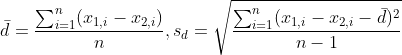
t-값은 다음과 같습니다.
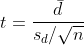
자유도는 n - 1 입니다.
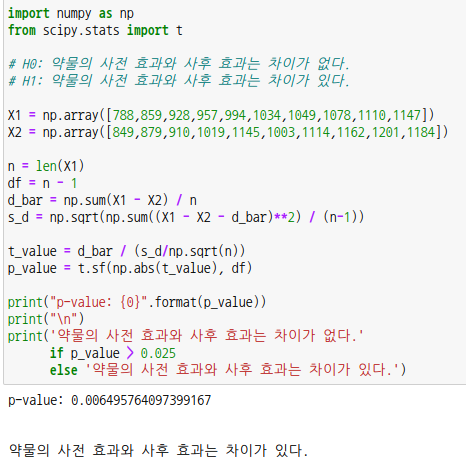
양측검증에 해당하고 p-값이 0.025보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다.
scipy 모듈의 서브패키지 ttest_rel 을 사용할 수도 있습니다. 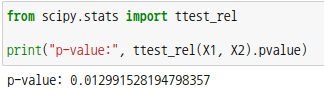
p-값이 0.05보다 작으므로 역시 귀무가설을 기각하고 대립가설을 채택합니다.
|  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟