
머신러닝 모델은 통계학을 기반으로 하기때문에 이번 글에서는 기본적인 통계학에 대해 알아보겠습니다.
1. 통계학의 기초
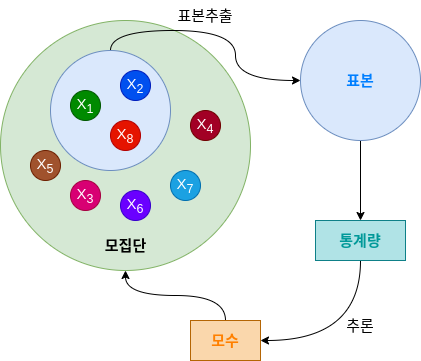
(1) 변수 : 개체의 특징을 나타내는 수치값입니다. (2) 모집단 : 정보를 얻고자 하는 대상이 되는 집단 전체를 말합니다.
(3) 표본 : 무작위로 추출된 모집단의 일부분을 말합니다.
(4) 모수 : 모집단의 특징을 나타내는 수치값입니다.
(5) 통계량 : 표본의 특징을 나타내는 수치값입니다. 평균, 중앙값, 최빈값, 분산 등과 같은 데이터를 대표하는 값이 이에 해당합니다. 개체수가 많으면 모수를 구하는데 많은 시간과 비용이 소모되므로 통계량을 통해 모수를 추정하게 됩니다.
통계적 특성 |
모수 |
통계량 |
개체수 |
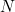
|
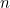
|
평균 |
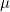
|
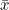
|
분산 |
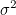
|
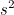
|
표준편차 |
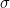
|

|
(6) 평균 : 집단의 변수를 전체 개체수로 나누어 얻는 통계량입니다.
모집단의 평균은 다음과 같습니다. 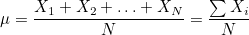
표본의 평균은 다음과 같습니다. 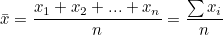
n = N일때 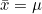 이므로 표본 개체수 n이 커질수록 표본평균 이므로 표본 개체수 n이 커질수록 표본평균 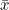 는 모평균 는 모평균 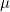 에 가까워집니다. 에 가까워집니다. 즉, 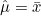 가 되므로 표본평균 가 되므로 표본평균 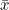 를 통해 모평균 를 통해 모평균 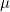 를 추정할 수 있습니다. ( 를 추정할 수 있습니다. (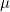 위에 ^은 hat이이고 읽으며, 추정값을 뜻합니다.) 위에 ^은 hat이이고 읽으며, 추정값을 뜻합니다.)
(7) 분산(variance) : 변수의 흩어진 정도를 나타내는 통계량입니다. 변수가 평균으로부터 떨어진 거리를 편차라고 하는데 편차제곱합의 평균값이 분산에 해당합니다.
모분산은 다음과 같습니다. 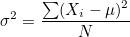
모분산의 경우 개체수로 나눠주지만 표본분산의 경우 자유도(degree of freedom; df)라는 값으로 나눠줍니다. 분산의 자유도는 n-1이므로 표본분산은 다음과 같습니다. 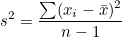
n이 아니라 (n-1)로 나누는 이유는 다음과 같은 과정으로 증명됩니다.
평균의 기대값을 E(X)라고 하면 분산 Var(X)는 변수 X와 E(X) 사이의 편차를 제곱하여 더한 값의 평균이 되므로 다음과 같이 정의할 수 있습니다.
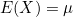 이므로, 이므로,
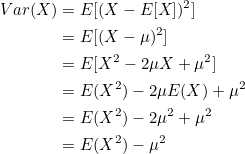
∴ 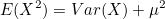
(1) 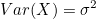 이므로, 이므로, 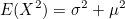
(2) 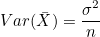 이므로, 이므로, 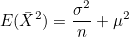
편차제곱합은 다음과 같이 정의할 수 있습니다.
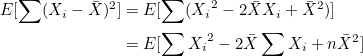
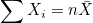 이므로, 이므로,
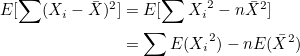
(1), (2)를 대입하면,
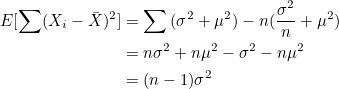
∴ 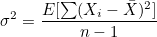
그러므로, 표본분산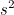 가 모분산 가 모분산 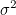 에 가까워지려면 표본의 편차제곱합 에 가까워지려면 표본의 편차제곱합 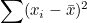 에 (n-1)을 나누어 주어야합니다. 에 (n-1)을 나누어 주어야합니다.
|
(8) 표준편차(standard deviation) : 분산의 제곱근입니다. 분산은 음의 부호를 제거하기위해 편차를 제곱하는 과정을 거칩니다. 그러므로 측정단위가 바뀌게 되므로 제곱근을 통해 단위를 되돌릴 수 있습니다. 예를 들어 변수가 원단위라면 분산은 원2이라는 단위가 됩니다. 원2이라는 단위는 존재하지 않는 단위이기 때문에 제곱근을 하여 다시 원단위로 되돌려줍니다.
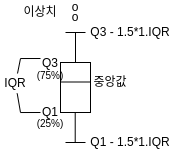
(9) 사분위수(quartile) : 데이터를 4등분한 값입니다. 25% 값을 1사분위수 (Q1), 50% 값을 2사분위수 (Q2), 75% 값을 3사분위수 (Q3) 라고 합니다.
(10) IQR : Interquartile Rage 약자이며, Q1과 Q3의 차이를 말합니다. 상자그림(box plot)에서 최소치와 최대치를 계산하기 위해 사용합니다.
2. 확률분포
(1) 확률(probability) : 해당 사건(event) 이 일어날 가능성을 의미합니다. 보통 실험적인 성향을 갖는 반복되는 시도를 통해 사건의 빈도수를 측정한 도수 확률(Frequentist probability)을 뜻합니다.
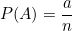
a는 사건 A가 일어난 횟수, n은 전체 시도 횟수입니다.
(2) 확률변수 : 사건을 나타내는 수치값입니다. 수치값이 정해져있는 이산확률변수와 모든 실수값을 가질 수 있는 연속확률변수로 분류됩니다.
(3) 확률분포 : 확률변수가 가질 수 있는 모든 값과 이 값이 나타날 확률을 정리한 것입니다. 이산확률변수의 확률분포를 이산확률분포라고 하며 확률 질량 함수(probability mass function; PMF)로 표현합니다. 연속확률변수의 확률분포를 연속확률분포라고 하며 확률밀도함수(probability density function; PDF)라는 연속곡선으로 표현합니다.
(4) 정규분포(normal distribution) : 다음 함수식을 가지는 연속확률분포를 말합니다.
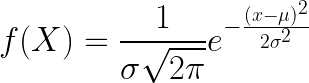
가우스가 처음 정립하여 가우스 분포(Gaussian distribution)라고도 부릅니다. 확률변수 X가 평균 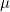 이고, 표준편차가 이고, 표준편차가 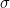 인 정규분포를 따를때 N( 인 정규분포를 따를때 N( 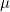 , , 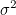 ) 로 표기합니다. ) 로 표기합니다.
정규분포는 평균 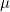 를 중심으로 좌우대칭인 종모양 곡선입니다. 위치는 평균 를 중심으로 좌우대칭인 종모양 곡선입니다. 위치는 평균 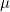 에 의해 결정되고, 분포모양은 표준편차 에 의해 결정되고, 분포모양은 표준편차 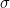 에 따라 달라집니다. 평균을 중심으로 좌우가 균등하므로 최빈값, 중앙값, 평균이 모두 동일합니다. 에 따라 달라집니다. 평균을 중심으로 좌우가 균등하므로 최빈값, 중앙값, 평균이 모두 동일합니다.
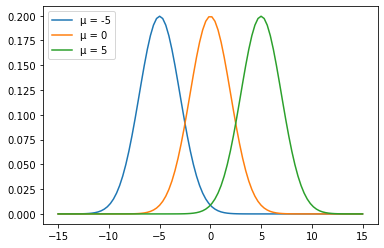
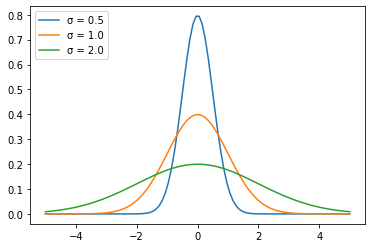
정규분포를 하는 변수는 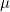 ± ± 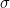 범위가 전체의 68.26%를 포함하고, 범위가 전체의 68.26%를 포함하고, 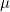 ± 2 ± 2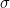 범위는 95.44%에 달합니다. 범위는 95.44%에 달합니다.
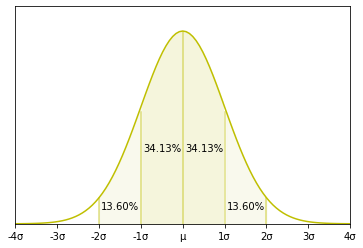
(5) 표준정규분포(standard normal distribution) : N(0, 1)인 정규분포를 말합니다. 확률변수로 Z값이 사용되는데, Z값은 편차를 표준편차로 나눈 값입니다.
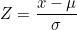
Z값이 확률변수 역할을 하므로 Z-분포라고도 부릅니다. 어떤 정규분포든지 표준화를 통해 N(0, 1)인 정규분포가 되므로 평균과 표준편차만 알면 표준정규분포표를 이용함으로써 확률을 계산할 수 있습니다.
예제로 다음 문제를 한번 풀어보겠습니다.
벼키(간장)은 정규분포하며 300개체에 대한 벼키의 평균이 64cm, 표준편차가 4cm이다. 벼키가 56cm와 72cm 사이에 있을 개체수는 얼마인가? |
주피터 노트북으로 풀어보겠습니다. 56cm와 72cm에 대한 z값을 구하여 norm 모듈의 cdf 함수를 통해 z값을 구합니다.

z값을 알면 norm 모듈의 cdf 함수를 통해 확률을 구할 수 있습니다. cdf는 cumulative distribution function의 약자로 표준정규분포에서 x값에 대한 누적확률을 출력합니다. 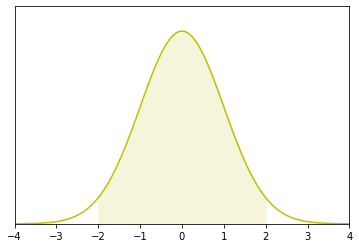
노란색 영역의 확률을 구해야하므로 cdf(2)에서 cdf(-2)를 빼면 누적확률이 출력됩니다.
이 값에 개체수 300을 곱하면 56cm ~ 72cm 길이를 갖는 개체수를 추정할 수 있습니다. 소수점이 나오므로 올림을 해주도록 합니다.
3. 표본분포
(1) 표본분포 : 표본의 통계량을 확률변수로 하는 확률분포를 말합니다.
어떤 모집단에서 크기가 n인 모든 표본을 추출하여 표본평균들의 평균을 구하면 모집단의 모평균과 같습니다.
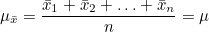
표본평균의 분산은 모분산을 표본크기로 나눈것과 같습니다.
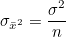
모집단이 정규분포를 보이면 표본평균들의 분포도 정규분포를 합니다. 즉, 모평균이 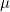 이고 모분산이 이고 모분산이 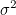 인 정규분포 모집단에서 크기가 n인 표본을 취하여 얻은 표본평균들은 평균이 인 정규분포 모집단에서 크기가 n인 표본을 취하여 얻은 표본평균들은 평균이 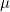 이고 분산이 이고 분산이 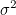 / n 인 정규분포를 따르며, 기호로 N( / n 인 정규분포를 따르며, 기호로 N(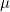 , , 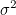 / n)라고 나타냅니다. / n)라고 나타냅니다.
모집단이 정규분포를 하지 않더라도 표본 크기가 30 이상이 되면 평균의 표본분포는 정규분포에 가까워지며, 이때 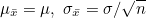 입니다. 이를 중심극한정리라고 합니다. 입니다. 이를 중심극한정리라고 합니다.
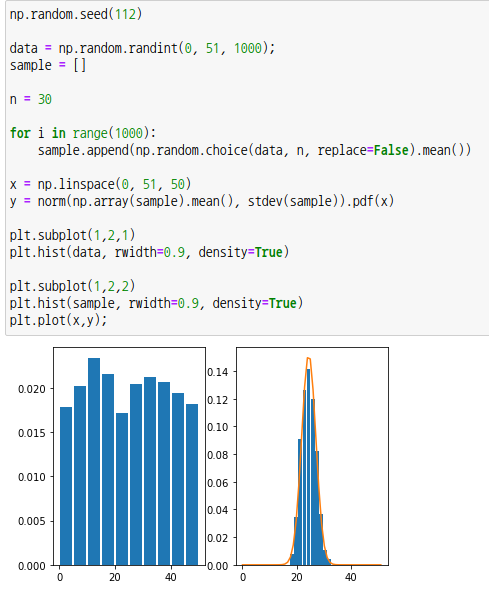
왼쪽 히스토그램은 0부터 50까지의 숫자를 무작위로 1000번 추출했을때 각 숫자가 나온 확률을 나타냈으며 정규분포를 하지 않고 있습니다. 모집단이라고 보면 됩니다.
오른쪽 히스토그램은 모집단에서 크기가 30인 표본을 1000번 추출했을때 표본평균이 나온 확률을 나타냈으며, 모집단이 정규분포를 하고 있지 않더라도 표본평균의 평균은 정규분포를 하고 있는 것을 볼 수 있습니다. 즉, 표준화가 가능합니다.
(2) 표준오차(standard error) : 표본평균들의 표준편차를 의미합니다. 표준편차는 모집단이 어느정도 흩어져 있는가를 설명하는 수치라면 표준오차는 표본평균이 어느정도로 불확실한가를 나타내는 나타내는 수치입니다. 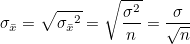
표준 오차를 구하기 위해서는 같은 모집단으로부터 크기가 n인 표본을 계속 추출해야하지만 단일표본에서 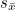 를 구하여 표준오차를 추정할 수 있습니다. 를 구하여 표준오차를 추정할 수 있습니다.
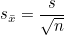
n값이 커지면 표준오차가 작아지므로 보다 정확한 추정값을 얻을 수 있습니다.
(3) t-분포 : 모분산 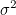 를 모르거나 표본크기 n이 작을때(n<30) 정규분포 대신에 사용하는 분포입니다. t값은 표본평균의 편차 를 모르거나 표본크기 n이 작을때(n<30) 정규분포 대신에 사용하는 분포입니다. t값은 표본평균의 편차 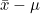 를 표준오차 를 표준오차 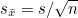 로 나누어준 값입니다. 로 나누어준 값입니다.
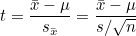
확률 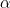 와 자유도 df에 대한 t값은 와 자유도 df에 대한 t값은 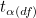 라고 표기합니다. 라고 표기합니다.
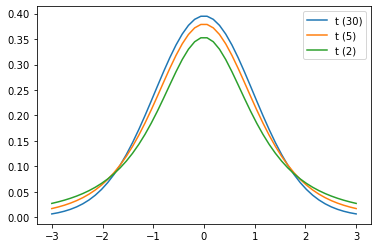
정규분포와 비슷하게 생겼으나 자유도에 따라 분포모양이 달라집니다. 자유도가 커질수록 정규분포에 가까워지며, 자유도가 무한대이면 정규분포와 일치하게 됩니다.
예제로 다음 문제를 한번 풀어보겠습니다.
생후 100일 된 돼지의 평균 체중은 50kg으로 알려졌으나 분산이 얼마인지는 모른다. 목장에서 16마리를 랜덤으로 추출하여 체중을 측정한 결과 평균 58kg이고 분산 81이었다. 생후 100일된 돼지들 중에서 16마리를 반복적으로 추출하여 평균을 구했을 때 58kg보다 더 큰 돼지가 나올 확률은 얼마인가? |

(4) χ²-분포 : 표준정규분포의 확률변수 Z값을 제곱한 확률분포입니다.
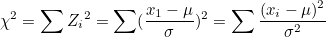
이 식에서 모평균 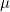 대신에 표본평균 대신에 표본평균 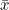 로 바꿔주면 χ²값들은 자유도가 n-1인 χ²-분포를 따르게 됩니다. 로 바꿔주면 χ²값들은 자유도가 n-1인 χ²-분포를 따르게 됩니다.
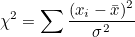
그런데 표본분산 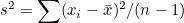 이므로 이므로 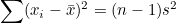 입니다. 이 식을 위에 식에 대입하면 다음과 같이 됩니다. 입니다. 이 식을 위에 식에 대입하면 다음과 같이 됩니다.
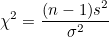
이 식은 χ²-분포가 표본분산의 분포임을 말해줍니다.
χ²-분포는 t-분포와 같이 자유도에 달라지지만, t-분포가 좌우대칭임에 반하여 χ²-분포는 비대칭적입니다. 또한 χ²-분포는 항상 0보다 큰 값을 가집니다. 자유도가 커질수록 정규분포에 가까워집니다.
χ²-분포는 표본분산의 분포로서 모분산에 대한 신뢰구간을 구할 수 있고, 모분산비가 표본분산비와 같은지 검정할 수 있습니다. 특히 이산형 변수의 통계분석에 많이 이용됩니다.
|  스팟
스팟