
F-값은 두 표본집단의 분산비(variance ratio)를 나타낸 값입니다. 즉, F-값을 통해 두 집단의 분산이 같은지 검정할 수 있습니다.
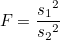
χ²-값은 표본집단의 분산을 표준화한 값이므로 일종의 분산입니다. 그러므로 다음과 같이 나타낼 수 있습니다.
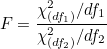
자유도가 2개 있으므로 F-값의 확률분포는 자유도가 (df1, df2)인 F-분포를 따릅니다.
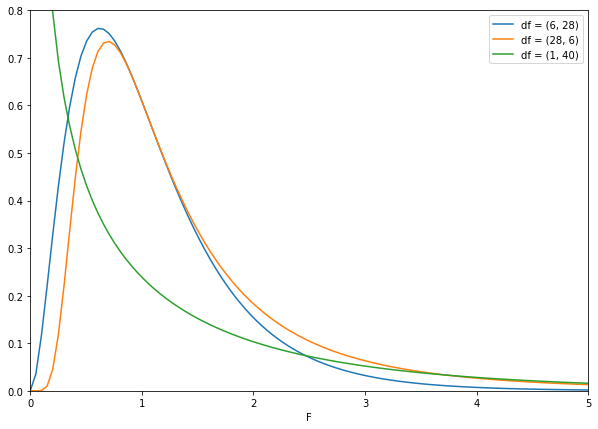
χ²-분포와 비슷한 모습을 보입니다. 분산비 이므로 양수만 존재합니다. 분포의 정점이 왼쪽으로 치우쳐 있으나 자유도가 증가함에 따라 점점 대칭에 가까워집니다.
F-값은 분산분석(ananlysis of variance, ANOVA)에 이용됩니다. t-검정과 마찬가지로 표본집단의 평균을 비교할 수 있는데 t-검정은 두 표본집단의 평균만 비교할 수 있는 반면 분산분석은 두 표본집단 이상의 평균을 비교할 수 있습니다. F-값을 이용하므로 ANOVA를 F-검정이라고 부릅니다.
t-검정을 한번 할때 유의수준 5%에서 제 1종오류가 발생하지 않을 확률은 95% 입니다. 그러므로 비교할 집단의 수가 증가할수록 오류가 누적되어 잘못된 결론을 내리게 될 확률이 증가하는데 ANOVA를 통해 여러집단을 한번에 비교하여 이 문제를 해결할 수 있습니다.
ANOVA를 하기 위해서 독립표본 t-검정처럼 독립성, 정규성, 등분산성의 전제조건이 필요합니다.
1개의 특징을 비교분석하는 일원배치 분산분석(one-way ANOVA), 2개 이상의 특징을 비교분석하는 이원배치 분산분석(two-way ANOVA)가 있는데 여기서는 일원배치 분산분석을 하겠습니다.
t개의 표본집단에서 n개체씩 조사하여 얻는 데이터는 다음과 같이 정리합니다.
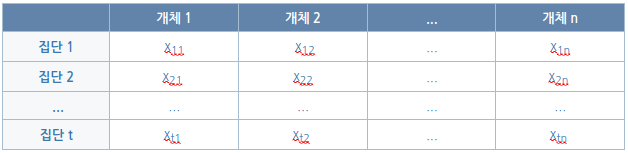
ANOVA에서는 집단을 처리(treatment), 개체를 반복(replication)이라고 부릅니다. t처리 n반복으로 정리하는 것을 일원분류(one-way classification)이라고 합니다.
우선 관찰값 xij 에 대해 알아봅시다. i번째 처리의 j번째 반복에서 얻을 수 있는 xij의 값은 다음과 같은 식으로 표현할 수 있습니다.
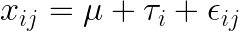
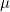 는 모평균, 는 모평균, 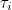 는 처리효과, 는 처리효과, 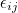 는 오차를 나타냅니다. 처리효과 는 오차를 나타냅니다. 처리효과 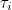 는 처리평균 는 처리평균 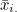 와 전체평균 와 전체평균 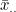 의 편차 의 편차 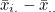 로 표시되며, 오차 로 표시되며, 오차 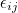 는 관찰값 xij 와 처리평균 는 관찰값 xij 와 처리평균 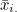 의 편차 의 편차 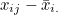 로 표시됩니다. 로 표시됩니다.
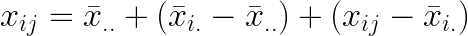
전체평균 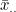 를 왼쪽 항으로 이동하면 다음과 같이 정리됩니다. 를 왼쪽 항으로 이동하면 다음과 같이 정리됩니다.

이식의 양변을 제곱하여 합하면 관찰값과 전체평균의 편차제곱합(sum of squares, SS)을 구할 수 있습니다.
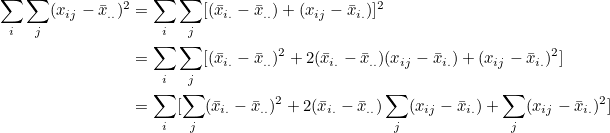
처리에서 처리평균에 대한 오차( 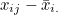 )를 모두 더한 값은 0이 됩니다. )를 모두 더한 값은 0이 됩니다.
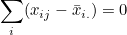
그러므로 다음과 같이 정리됩니다.
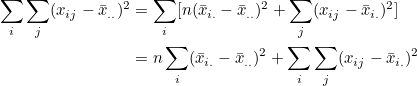
즉, 관찰값과 전체평균의 편차제곱합(sum of squares, SST)은 처리평균과 전체평균의 편차제곱합(treatment sum of squares, SSTr)과 관찰값과 처리평균의 편차제곱합(error sum of squares, SSE)으로 구성됩니다.
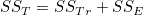
SST 를 총제곱합, SSTr 를 처리제곱합, SSE 를 오차제곱합이라고 합니다. 처리제곱합을 군간제곱합(sum of squares, between, SSB), 오차제곱합을 군내제곱합(sum of squares within, SSW)이라고도 합니다.
SST 는 다음과 같이 변형될 수 있습니다.
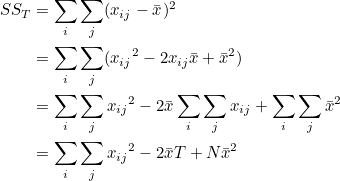
T는 전체 관찰값의 합이고, N은 전체 표본의 크기입니다. T = N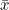 이므로 이므로 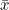 = T / N 입니다. = T / N 입니다.
그러므로 최종적으로 다음과 같이 나타낼 수 있습니다.
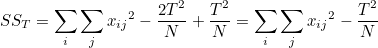
마찬가지로 SSTr 도 다음과 같이 변형될 수 있습니다.
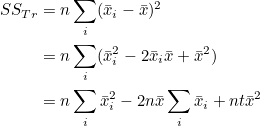
처리평균 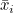 를 모두 더한 값을 반복수 t로 나누면 전체평균 를 모두 더한 값을 반복수 t로 나누면 전체평균 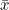 가 됩니다. 또한 처리내 관찰값을 모두 더한 값을 Ti 라고 하면 가 됩니다. 또한 처리내 관찰값을 모두 더한 값을 Ti 라고 하면 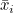 = Ti / n 이 됩니다. 그러므로 다음과 같이 정리됩니다. = Ti / n 이 됩니다. 그러므로 다음과 같이 정리됩니다.
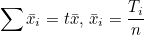
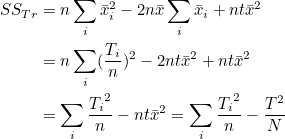
T2 / N 이 공통되어 나타납니다. 이 값을 보정항(correction term, CT)이라고 합니다. 즉, 결론은 다음과 같이 정리됩니다.
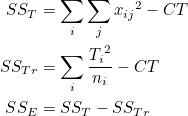
t처리 n반복에 대하여 총제곱합(SST)의 자유도는 tn-1 이고, 처리제곱합(SSTr)의 자유도는 t-1, 오차제곱합(SSE)의 자유도는 t(n-1) 입니다. 모두 분산을 나타내는 값이므로 각각 X2-분포를 따릅니다.
처리제곱합(SSTr)을 자유도 t-1로 나눈 값을 처리평균제곱합(treatment mean squares, MSTr)이라 하며, 오차제곱합(SSE)을 자유도 t(n-1)로 나눈 값을 오차평균제곱합(error mean squares, MSE)이라고 합니다.
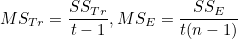
오차평균제곱합(MSE)의 기대값 E(MSE)는 오차분산, 처리평균제곱합(MSTr)의 기대값 E(MSTr)은 처리분산이 됩니다. 오차분산은 처리 간의 차이를 검정하는데 사용됩니다. 처리분산은 오차분산 이외에 처리효과로 인한 분산이 포함되어 있습니다. 즉, 처리평균( 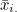 ) 사이에 차이가 없으면 처리효과( ) 사이에 차이가 없으면 처리효과(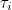 )가 없다는 뜻이 되므로 처리분산과 오차분산은 같은 값을 가지게 됩니다. 그러나 처리평균 사이에 차이가 있으면 처리분산의 크기가 오차분산보다 커지게 됩니다. 따라서 처리분산과 오차분산을 비교하면 "모든 평균은 동일하다"는 귀무가설을 검정할 수 있으며, 이때 F-값은 다음과 같습니다. )가 없다는 뜻이 되므로 처리분산과 오차분산은 같은 값을 가지게 됩니다. 그러나 처리평균 사이에 차이가 있으면 처리분산의 크기가 오차분산보다 커지게 됩니다. 따라서 처리분산과 오차분산을 비교하면 "모든 평균은 동일하다"는 귀무가설을 검정할 수 있으며, 이때 F-값은 다음과 같습니다.
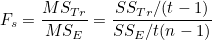
iris 데이터의 꽃받침 길이를 F-검정 해보겠습니다.
iris 데이터로부터 iris 종(species)을 기준으로 꽃받침 길이(sepal_lenth)를 출력하도록 데이터를 정리합니다. 행 인덱스는 처리를, 열 라벨은 반복을 나타냅니다. 처리마다 반복수가 다를 경우를 생각하여 코딩했습니다.
가설을 세우고 F-값을 구하여 F-검정을 해보세요.

scipy 모듈의 서브패키지 f_oneway 를 사용할 수도 있습니다.
파라미터로 처리 배열을 나열하면 됩니다. 아래에 *data는 data[0], data[1], data[2] 를 의미합니다.
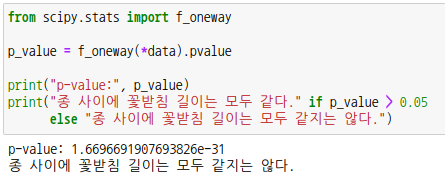
p-값이 0.05보다 작으므로 귀무가설을 기각하고 대립가설을 채택합니다. 이때 적어도 하나는 꽃받침 길이가 다르다라는 결론을 알수 있지만 어느 품종의 꽃받침 길이가 다른지 알기 위해서는 다른 검정절차를 거쳐야합니다. 여기서는 다루지 않겠습니다. |  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟