
회귀분석(regression analysis)은 변수들 간의 관계를 분석하여 하나의 변수값으로부터 다른 변수값을 예측하는 것을 의미합니다. 같은 개체에서 측정한 두 변수 사이에 관련성이 있을 때, 다른 변수에 영향을 주는 변수를 독립변수(independent variable), 독립변수에 의해 영향을 받는 변수를 종속변수(dependent variable)라고 합니다. 독립변수를 설명변수(explanatory variable), 종속변수를 반응변수(response variable)라고도 부릅니다. 두 변수 간에 상관관계가 높으면 독립변수는 종속변수를 더 잘 설명할 수 있고, 또한 독립변수의 값으로부터 종속변수의 값을 보다 정확히 예측할 수 있습니다. 그러므로 회귀분석은 상관분석을 바탕으로 이루어집니다.
회귀분석은 독립변수와 종속변수의 관계를 함수식으로 나타내는데, 이를 회귀방정식(regression equation)이라 하고, 회귀방정식을 직선으로 나타낸 것을 회귀직선(regression line)이라고 합니다.
1) 단순회귀분석(simple regression analysis)
단순회귀분석은 하나의 설명변수와 하나의 반응변수를 통해 관계를 분석합니다. 회귀방정식은 다음과 같습니다.
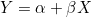
α 는 직선의 절편(intercept)이고, β 는 직선의 기울기(slope)입니다. β 는 독립변수(X)의 변화에 따른 종속변수(Y)의 변화량을 나타내며, 이것을 회귀계수(regression coefficient)라고 합니다.
회귀방정식은 실제 관찰값 y를 예측한 값이므로 추정회귀방정식으로 나타냅니다.
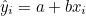
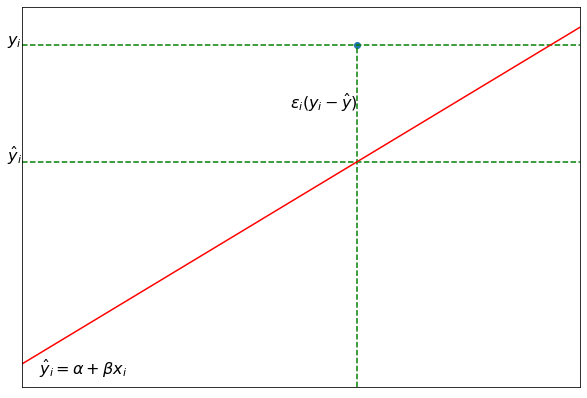
예측값 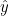 는 관찰값 y와 차이가 있으며, 그 차이를 오차(random error, ε) 또는 잔차(residual effect)라고 합니다. 따라서 실제 관찰값 y에는 오차 ε가 포함되어 있으므로 다음과 같이 표시할 수 있습니다. 는 관찰값 y와 차이가 있으며, 그 차이를 오차(random error, ε) 또는 잔차(residual effect)라고 합니다. 따라서 실제 관찰값 y에는 오차 ε가 포함되어 있으므로 다음과 같이 표시할 수 있습니다.
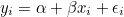
이 식을 변수 X에 대한 회귀모형(linear regression model)이라고 합니다. 추정회귀방정식을 회귀모형에 가깝도록 하기 위해서는 오차의 합이 최소가 되는 α와 β를 구하면 됩니다. 머신러닝에서는 오차를 손실(lost) 또는 비용(cost)이라 하며, 오차를 정의한 함수를 손실함수 또는 비용함수라고 합니다. 즉, 머신러닝에서 훈련이란 비용함수를 최소화 할 수 있는 α와 β를 구하는 과정을 말합니다. 보통 비용함수로써 평균제곱오차(mean square error, MSE)를 사용합니다.
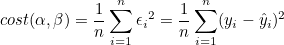
선형회귀모델에서는 최소제곱법(Least squares method, LSM) 또는 경사하강법(Gradient descent)을 통해 최적의 방정식을 구할 수 있습니다. 여기서는 최소제곱법을 이용하여 α와 β를 구해보도록 하겠습니다.
우선 비용함수는 2차함수이기 때문에 선형플롯으로 표현하면 다음과 같습니다. 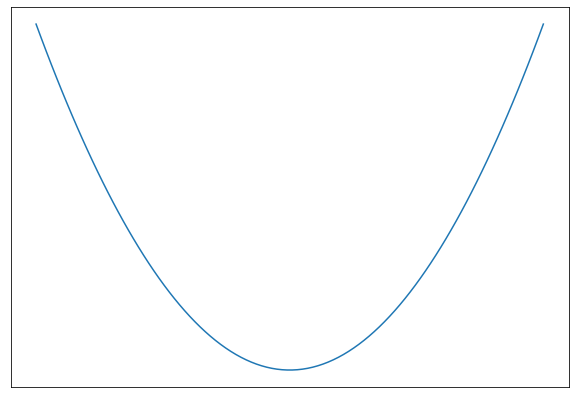
즉, 기울기가 0인 지점이 비용함수가 최소가 되므로 비용함수를 미분하여 0이 되는 지점을 찾으면 됩니다. 비용함수를 α와 β로 편미분합니다.
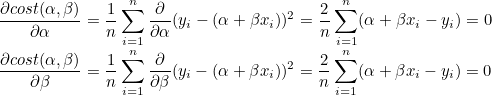
=>
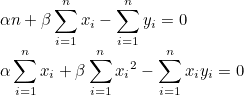
=>
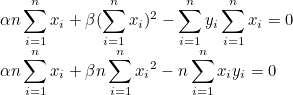
두 연립방정식을 합치면 β를 구할 수 있습니다.
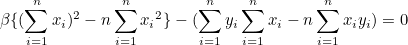
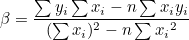
분자와 분모에 n을 나눠주면 다음과 같습니다.
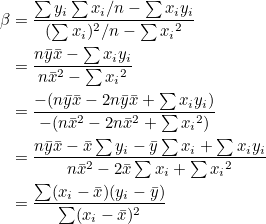
분자는 x 편차와 y편차를 곱하여 모두 합한 값이고 분모는 x 편차의 제곱합 입니다. 그러므로 분모와 분자를 자유도 n-1로 나누어주면 분자는 공분산, 분모는 분산이 됩니다.
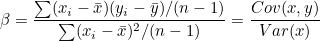
α는 첫번째 연립방정식으로부터 쉽게 구할 수 있습니다.
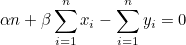
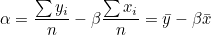
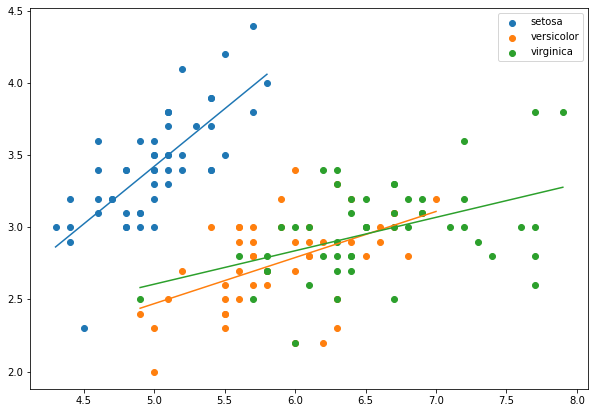
iris 데이터로부터 품종별로 꽃받침 길이에 대한 꽃받침 넓이의 회귀직선을 그려보겠습니다.

2) 다중회귀분석(multiple regression analysis)
다중회귀분석은 둘 이상의 설명변수와 하나의 반응변수를 통해 관계를 분석합니다. 회귀방정식은 다음과 같습니다.
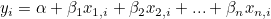
다중회귀는 n차원의 설명변수와 1차원의 반응변수로 총 n+1차원을 가지며, 1차원 낮은 n차원의 초평면을 형성합니다. 최적의 모델을 얻기 위해서 단순회귀처럼 비용함수를 최소화하는 회귀계수들을 구해야합니다.
독립변수가 2개인 경우를 예를 들면 비용함수는 다음과 같이 형성됩니다. 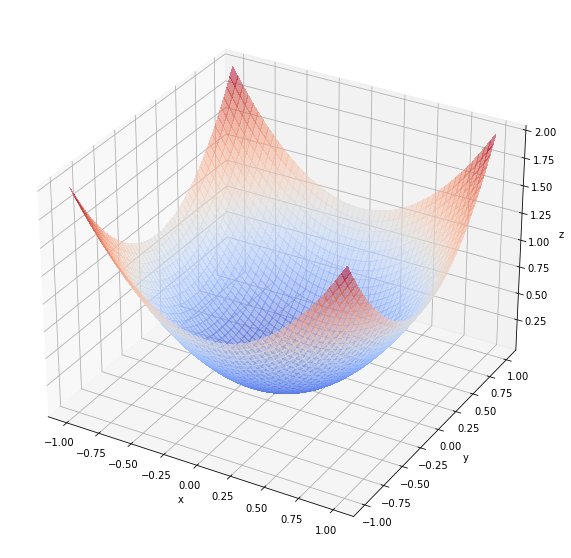
해당함수에 접하는 면의 기울기가 0인 지점이 비용함수가 최저인 지점이 됩니다.
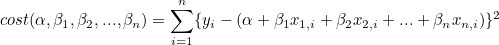
너부 복잡한 식입니다. 해당 식을 벡터로 변형하도록 하겠습니다. 우선 선형연립방정식을 만들어봅시다.
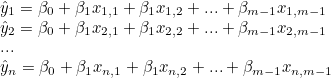
선형연립방정식은 다음과 같이 행렬의 곱으로 나타낼 수 있습니다.

종속변수 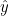 는 n x 1 열벡터, 독립변수 X는 n x m 행렬, 는 n x 1 열벡터, 독립변수 X는 n x m 행렬, 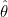 는 m x 1 열벡터 입니다. 는 m x 1 열벡터 입니다.
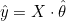
비용함수는 다음과 같습니다.
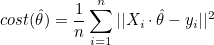
n차원 공간에서 벡터의 크기(노름) ||X||2 은 XTX 와 같습니다. XT는 X의 전치행렬(transpose matrix)을 말합니다. 즉, 행과 열을 전환한 행렬입니다.
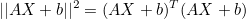
전치행렬의 성질은 다음과 같습니다.
(AT)T = A (A + B)T = AT + BT (kA)T = kAT (k는 스칼라값) kT = k (AB)T = BTAT |
Xi는 행렬 X의 i번째 행벡터 이고, 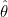 는 열벡터 이므로 다음과 같이 나타낼 수 있습니다. 는 열벡터 이므로 다음과 같이 나타낼 수 있습니다.
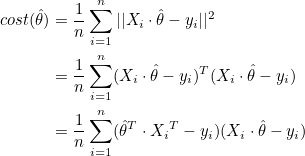
비용함수의 최소값을 찾으려면 비용함수를 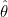 로 편미분한 값이 0인 경우를 찾으면 됩니다. 로 편미분한 값이 0인 경우를 찾으면 됩니다. 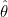 은 열벡터이므로 행벡터로 전치시켜서 미분합니다. 은 열벡터이므로 행벡터로 전치시켜서 미분합니다.
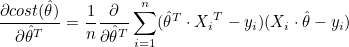
곱의 미분법 공식은 다음과 같습니다.
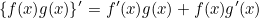
이것을 이용하여 다음과 같이 미분할 수 있습니다.
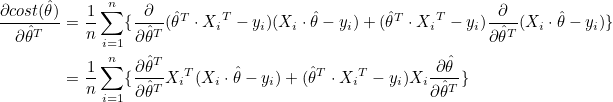
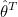 는 1 x m 행벡터, 는 1 x m 행벡터, 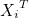 는 m x 1 열벡터이므로 는 m x 1 열벡터이므로 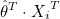 는 스칼라값이 됩니다. 는 스칼라값이 됩니다.
또한 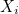 는 1 x m 행벡터, 는 1 x m 행벡터, 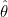 는 m x 1 열벡터이므로 는 m x 1 열벡터이므로 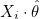 도 스칼라값이 됩니다. 도 스칼라값이 됩니다.
그러므로 뒤에 미분한 값은 전체적으로 스칼라 값이므로 전치시켜도 값이 같습니다.
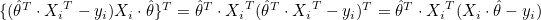
뒤에 미분한 값이 앞에 미분한 값과 같으므로 다시 정리하면 다음과 같습니다.
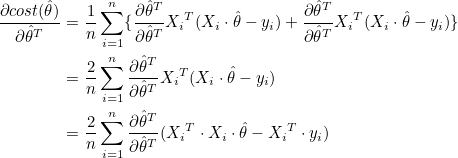
그러므로 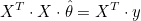 일때 면의 기울기는 0이 됩니다. XTX 는 m x m 행렬이므로 정방행렬이고, 역행렬을 가질 수 있습니다. 양변에 (XTX)-1을 곱하면 θ 를 구할 수 있습니다. 일때 면의 기울기는 0이 됩니다. XTX 는 m x m 행렬이므로 정방행렬이고, 역행렬을 가질 수 있습니다. 양변에 (XTX)-1을 곱하면 θ 를 구할 수 있습니다.
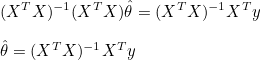
 의 첫번째 성분은 절편에 해당하고 나머지 성분은 초평면의 기울기(gradiant)에 해당합니다. 의 첫번째 성분은 절편에 해당하고 나머지 성분은 초평면의 기울기(gradiant)에 해당합니다.
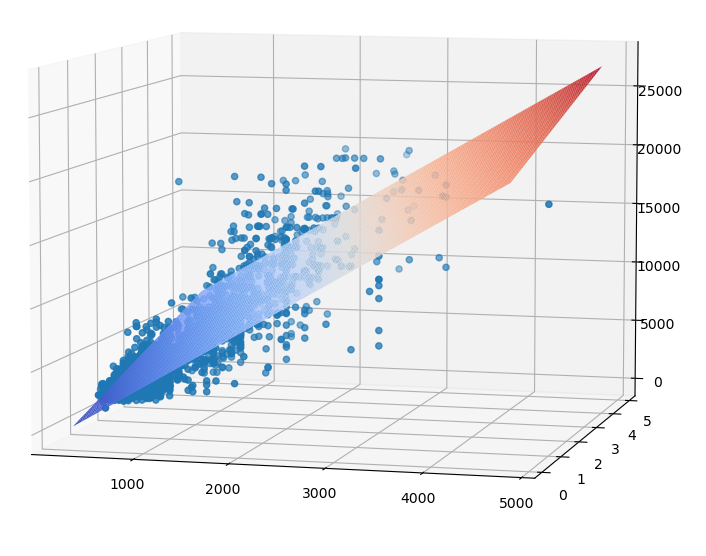
맨허튼 집값 데이터를 통해 그라디언트를 구하고 초평면을 그려보도록 하겠습니다. numpy 모듈의 linalg.inv 함수를 통해 역행렬을 구할 수 있고, 행렬의 곱은 @를 적어주면 됩니다.

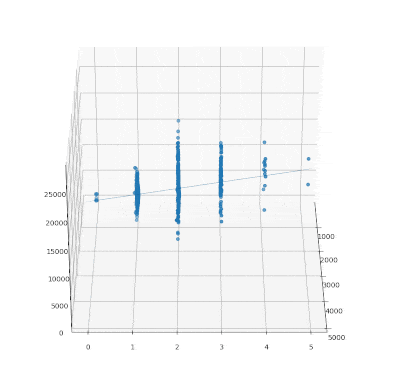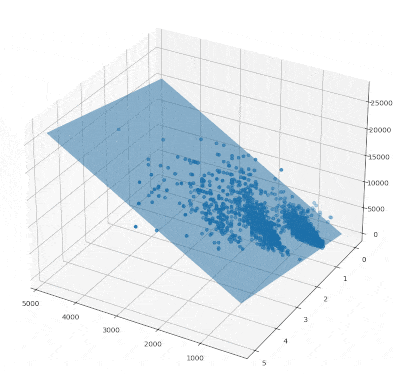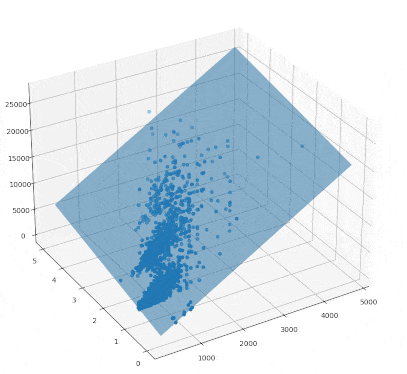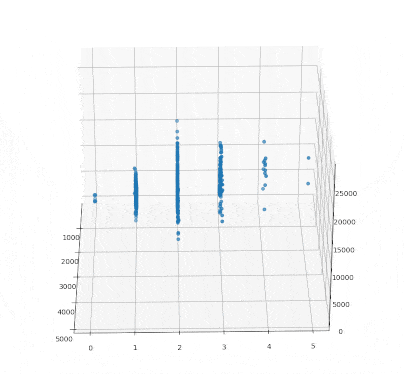
|  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟