
1. 로지스틱 회귀(Logistic Regression)
선형회귀는 설명변수와 반응변수 사이에 상관관계가 있다는 가정에 의해 형성될 수 있습니다. 설명변수와 반응변수가 연속형 데이터인 경우 다음과 같이 선형회귀로 데이터를 설명할 수 있습니다. 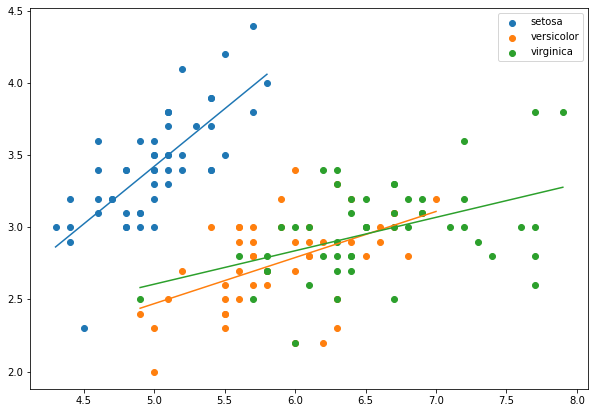
범주형 데이터인 경우 보통 1(True)과 0(False)으로 치환하여 데이터를 표현합니다. 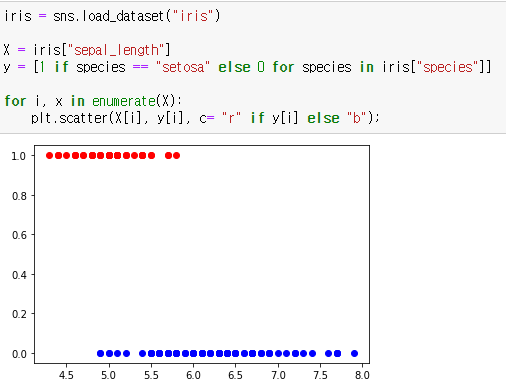
해당 데이터를 선형회귀로 나타내면 다음과 같은 회귀선이 나옵니다.
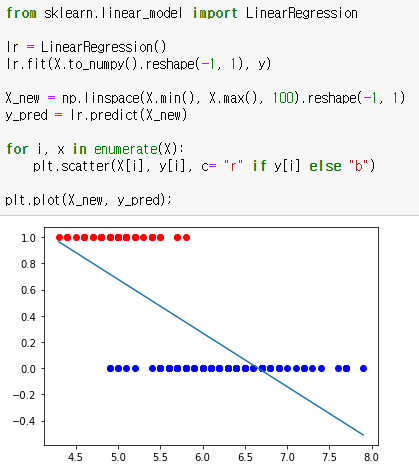
반응변수 y는 0과 1 사이의 확률로써 나타나기때문에 이와 같은 선형회귀로는 범주형 데이터를 설명할 수가 없습니다.
이런 범주형 데이터는 시그모이드 함수(Sigmid function)라는 S자형 함수를 통해 설명할 수 있습니다. 대표적으로 로지스틱 함수(Logistic function)가 있습니다.
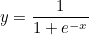
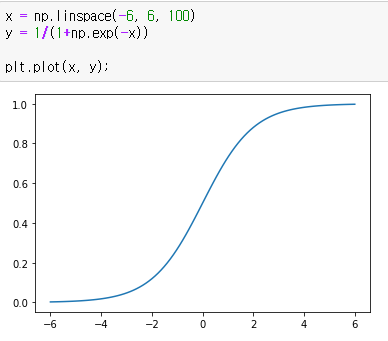
즉, 로지스틱 함수를 통한 반응변수의 예측을 로지스틱 회귀(Logistic Regression)라고 합니다.
2. 로지스틱 함수(Logistic function)
로지스틱 함수는 베르누이 시행에서 시작됩니다. 베르누이 시행은 0과 1 두가지 결과만이 나타나게 되는 실험을 말합니다. 예를 들어, 동전을 던지면 앞면 또는 뒷면 2가지 결과만이 나오게 되며, 동전을 던지는 행위를 베르누이 시행이라고 합니다. 베르누이 시행의 확률분포는 정규분포를 합니다.
베르누이 시행에서 1이 나올 확률을 x 라고 한다면 0이 나올 확률은 1 - x 가 됩니다. 0이 나올 확률에 대한 1이 나올 확률의 비를 승산비(odds raito)라고 합니다.
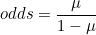
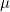 의 범위는 0 ~ 1이므로 승산비의 그래프를 나타내면 다음과 같습니다. 의 범위는 0 ~ 1이므로 승산비의 그래프를 나타내면 다음과 같습니다.
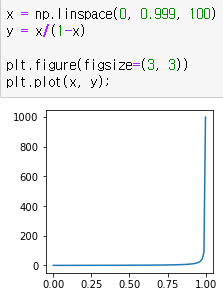
승산비에 자연로그를 취하면 다음과 같은 그래프가 됩니다.
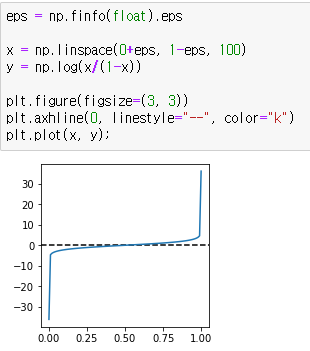
이때 함수식을 g(x)라고 하면 g(x)는 다음과 같습니다.
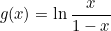
g(x)는 -∞ ~ ∞의 값을 가질 수 있으므로 선형회귀가 가능하며, 이를 로지트 함수(Logit function)라고 합니다.
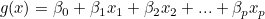
승산비를 p(x)라고 할 때, 로지트 함수에 승산비를 대입하면 다음과 같이 됩니다.
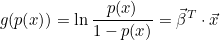
이때 p(x)는 로지트 함수 g(x)의 역함수가 되며, p(x)를 다음과 같이 유도할 수 있습니다.
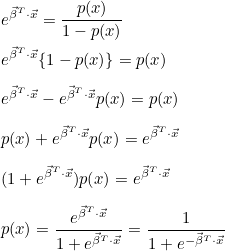
로지스틱 함수가 되었습니다! 즉, 로지스틱 함수는 로지트 함수의 역함수이며, 승산비라는 것을 알 수 있습니다. 로지스틱 함수 상태로는 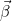 의 의미를 직관적으로 알기 어렵지만 선형회귀식인 로지트 함수로 변형하면 의 의미를 직관적으로 알기 어렵지만 선형회귀식인 로지트 함수로 변형하면 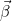 는 단위 x 당 승산비의 자연로그값의 그라디언트(gradiant)라는 것을 알 수 있습니다. 는 단위 x 당 승산비의 자연로그값의 그라디언트(gradiant)라는 것을 알 수 있습니다.
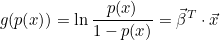
정리하면, 로지스틱 모델은 선형 모델인 로지트 함수를 비선형 모델인 로지스틱 함수로 표현한 모델입니다.
3. 최대우도추정법(Maximum Likelihood Estimation, MLE)
최대우도추정법이란 확률밀도함수에서 관측된 데이터를 기반으로 확률변수의 모수를 추정하는 방법입니다. 예를 들어서 동전을 10번 던져서 6번 앞면이 나왔을때 앞면이 나올 확률을 구하는 것입니다.
우선 동전을 던지는 것은 베르누이 시행에 해당하고, 앞면이 나올 확률은 이항분포를 나타냅니다. 이항분포에 대한 확률밀도함수는 다음과 같습니다.
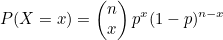
n은 베르누이 시행 횟수이고, x는 성공 횟수입니다. 함수식을 작성하면 다음과 같습니다.
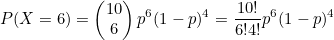
이때 P(X=6)를 우도(Likelihood) 라고 합니다. p값에 따라 우도가 달라지며, 이때 우도의 최대지점에서 확률 p가 있을 확률이 가장 높은 점이라고 추정합니다. 이항분포는 정규분포를 하고 있으므로 미분한 값이 0이 되는 지점이 최대지점입니다. 곱셈이 많아서 계산이 힘드므로 양변에 자연로그를 취해줍니다.
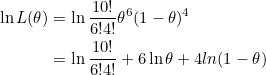
양변을 θ 로 미분합니다.
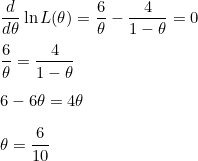
즉, 확률 p는 0.6이라고 추정할 수 있습니다.
마찬가지로 로지스틱 함수의 파라미터 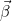 도 최대우도추정법을 통해 추정할 수 있습니다. 도 최대우도추정법을 통해 추정할 수 있습니다.
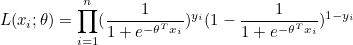
∏는 무한곱을 뜻하며, i=1 부터 n까지 모든 항을 곱하라는 뜻입니다. 즉, xi 에 대한 모든 우도를 곱한 값이 n번의 독립시행에 대한 우도입니다. 양변에 자연로그를 취하고 로지스틱 함수를 π(x) 라고 정의합시다.
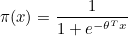
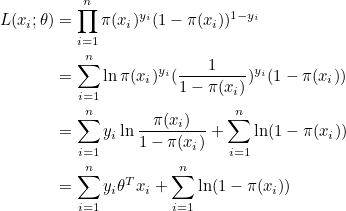
양변을 θ 로 미분합니다.
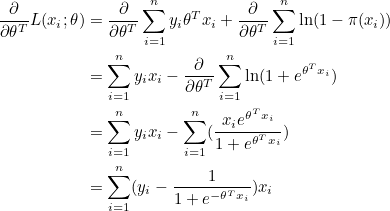
그라디언트 ∇L(xi; θ) 가 0이 되는 지점이 우도의 최대값인데, θ 에 대한 그라디언트가 비선형 관계에 있어서 선형함수처럼 쉽게 θ 를 구할 수 없습니다. 그러므로 경사하강법(gradient descent) 같은 수치적 최적화(numerical optimization)를 통해 최적의 θ 를 구해야하는데 이번 글에서는 설명하지 않겠습니다.
4. 파이썬 연습
지난번 사용한 ctr 데이터를 사용하여 로지스틱 회귀를 통해 분류해보겠습니다. 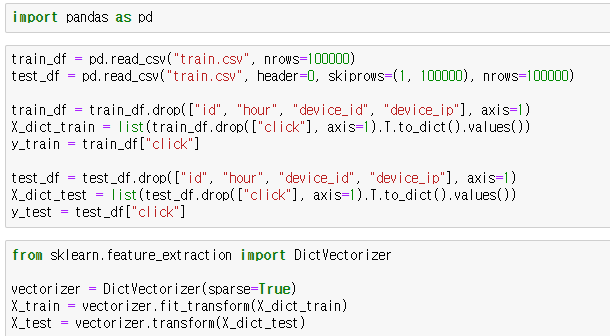
사이킷런 모듈의 LogisticRegression 함수를 통해 로지스틱 모델을 생성할 수 있습니다. 하이퍼 파라미터에 C는 규제 강도의 역수를 설정하고, penalty는 규제 방법을 선택합니다. 규제에 대해서는 이 글에서 설명하지 않겠습니다. 모델의 과적합을 막는 수단이라 보시면 됩니다.
solver는 최적화 알고리즘을 설정하는데 사이킷런 모듈의 버전이 바뀌면서 default 값이 lbfgs 로 바뀌었습니다. lbfgs로 설정하면 속도는 빠르지만 성능이 조금 떨어져 solver를 liblinear로 설정했습니다. 대신 학습 속도는 느립니다. lbgfs는 l2 규제만 사용하므로 lbgfs를 사용하려면 penalty 파라미터에서 l1은 지워주세요.
그리드 서치의 scoring의 경우 로지스틱 모델에서는 ng_log_loss 라는 크로스 엔트로피(cross entropy)를 사용하기도 합니다. 말그대로 엔트로피 지수이기때문에 낮을수록 잘 분류된 모델입니다.
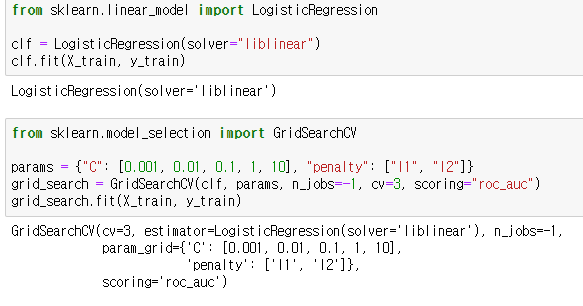
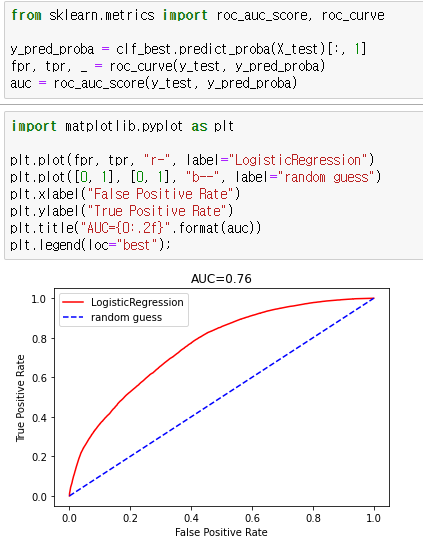
최적의 모델을 통해 정확도와 혼동행렬을 확인해봅시다.
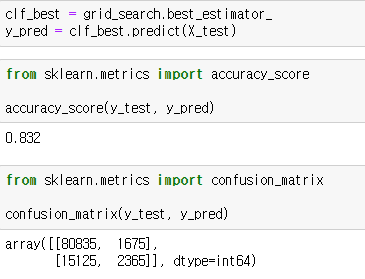
어느정도 분류는 되지만 랜덤포레스트보다는 점수가 조금 떨어지네요.
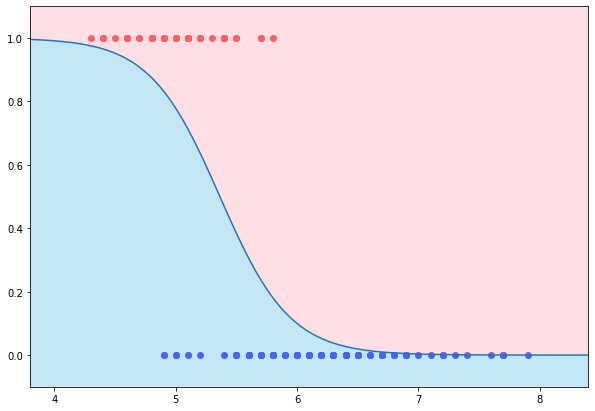
처음으로 돌아가서, 아이리스 품종을 "setosa"와 그외 품종으로 분류해봅시다.

|  스팟
스팟  스팟
스팟  스팟
스팟  스팟
스팟